A much more comprehensive discussion of techniques with a nifty solver program can be found here. There is also some very helpful discussion of Sudoku techniques at BrainBashers. What follows is a work in progress. There are explanations of the basic scanning and analysis techniques. More will be added as time goes on.
Before describing the techniques, I should explain the distinction between scanning and analysis. I borrowed the idea from the Wikipedia article. In some respects the distinction is artificial, but when writing a computer program to solve Sudoku puzzles, the distinction takes on some significance.
Scanning techniques identify where a digit must go by one of 2 lines of reasoning: first, a digit must go in a cell if no other digit can go in that cell; and second, a digit must go in a cell if there is no other cell where the digit can go (e.g. there is only one cell in a row that can receive the digit 4, but every row must have the digit 4 in it exactly once, so the 4 must be placed in that cell).
Analysis techniques identify where a digit cannot go, that is, it eliminates a digit from the candidates set(s) of one or more cells. Analysis usually proceeds by identifying a set of cells (usually 2 or 3 cells) with the properties: 1) that a certain digit must appear in at least one cell of the set, and 2) that the set has at least one common buddy. Every row, column and block has the first property by definition (in fact the definition is more restrictive, requiring each digit to appear in exactly one cell), but techniques of analysis allow us to identify other sets of cells with this property, such as a subset of a row, column or block or even cells that have no row, column or block in common. If a digit must appear in at least one cell of the set then that digit can be eliminated from the candidate sets of all the common buddies of the set.
- missing digit scan:
- Pick an empty cell, then scan its buddies. If all but one of
the digits (1-9) are present, then the missing digit must go in
the empty cell. In other words, a missing digit scan is looking
for empty cells with only one candidate. When a cell has only
one candidate, no other digit but the one remaining candidate
can go in that cell, so it must go there if the puzzle has a
solution.
A missing digit scan on the empty cell at the intersection of the 4th row and 5th column (green tinted cell) in the illustration below reveals that its buddies (red tinted cells) contain all the digits from 1 to 8. Therefore 9 is the only remaining candidate and must go in the empty cell.
A missing digit scan reveals that a 9 belongs in the green tinted cell.




In general, any time a cell’s candidate set is reduced to only one member even though the cell’s buddies may not contain all the other digits, the missing digit scan detects that there is only one candidate and changes its status from candidate to the solution for that cell.
The missing digit scan is the easiest technique to grasp. It flows logically and naturally from the rules of Sudoku itself. But it is not the easiest technique to use. Consider that there are 81 cells each with 20 buddies. Of the 81 cells, you probably start with an average of 56-60 cells to fill in. The sheer numbers are daunting. Do you really want to examine 56 to 60 sets of 20 cells each? Hence, although this is the most obvious technique, my program gives it a higher difficulty rating than the other basic scanning technique.
- cross-hatching:
- The other basic scanning technique is cross-hatching. Pick a
digit, then draw a line through the rows and columns containing
that digit, and scratch out the blocks that contain it too. The
empty cells that are not crossed out or scratched out are
potential locations for that digit. If only one potential
location exists in a row, column or block then the digit must
go there.
Cross-hatching the 4s reveals the location of 2 more 4s.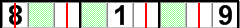



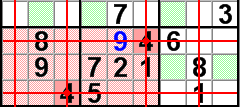




In the illustration above the empty cells that weren't eliminated by cross-hatching the 4s (the red lines and red tinted blocks) are tinted green. So the green tinted cells potentially could contain a 4. When we examine the block in the center of the bottom band, we see that there is only one green cell in it. A 4 must be placed here, because it cannot be placed in any other cell in the block. When we examine the center (5th) column we see that it too has only one green cell. A 4 must be located here because it is the only cell in the column where a 4 is allowed.
Cross-hatching becomes much simpler when you only consider one chute at a time. In the previous example, if we just considered the bottom band, it would be immediately obvious that there are 4s in the bottom 2 rows. One of the 4s is in the left block, the other in the right block. This leaves a 4 to be found in the center block and we know it must go in the top row. There is already a 3 in the center cell, so the 4 must go in either the left or right cell. Looking up the columns, we see a 4 in the right column and that only leaves the cell on the left.
A simpler approach to cross-hatching; cross-hatching a block.




The previous example of simplified cross-hatching is also an example of cross-hatching the bottom center block. We didn’t start out with a particular block in mind, but our attention was drawn to it by the fact that only one 4 remained to be found in the bottom band. We say that we cross-hatched the block because we examined the block to see where a 4 could be placed and discovered that there was only one cell in the block that could receive a 4. Oddly enough, this is also an example of cross-hatching a row. If we had instead focused on the 7th row, we would see that there is a 4 in the bottom left block which eliminates 4 as a candidate for the first 3 cells on the left of the 7th row, there is a 4 in the bottom right block which eliminates the possiblity of a 4 in the right-most 3 cells of the row, and there is a 4 in the 6th column which leaves only one empty cell in the 7th row that can receive a 4.
When we focus on the center (5th) column, we notice that all the rows intersecting the empty cells in the center column have 4s in them except the 2nd row. This is an example of cross-hatching a column. Again, we say that we cross-hatched the center column because we examined it to see where a 4 could be placed and found there was only one cell in the column that could receive a 4.
A simpler approach to cross-hatching; cross-hatching a column.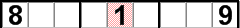




It is my experience that cross-hatching blocks is noticeably easier than cross-hatching rows or columns, hence my program assigns a higher difficulty score to cross-hatching the rows and columns than to cross-hatching the blocks.
- virtual cross-hatching:
- Originally I called this technique region intersection
analysis, however virtual cross-hatching is an even more
descriptive name. In the illustration below consider what we
learn from cross-hatching the 4s. Notice that the 4s in the
8th column and the 2nd row restrict the
location of the 4 in the upper right block to the 1st and 3rd
cells of the 7th column. Since there must be a 4 in
one of those 2 cells (because there must be a 4 in the block),
there cannot be a 4 in the rest of the 7th column.
That is an example of virtual cross-hatching.
Cross-hatching the 4s plus virtual cross-hatching reveals the location of another 4.
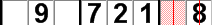


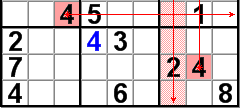
Continuing with the illustration above, cross-hatching alone leaves us with 2 potential locations for the 4 in the middle block of the stack on the right, but virtual cross-hatching eliminates the possiblity of a 4 in the 7th column, leaving only one possible location for the 4.
Virtual cross-hatching begins by looking at the intersection of 2 regions formed either by the intersection of a row and a block, or a column and a block. If a candidate digit is limited in a row to only cells in one of the blocks the row intersects, then that digit may be eliminated as a candidate from all cells in the block that are not in the row. Likewise for a column and a block. Alternately, if a candidate digit is limited to a single row or column of a block, that candidate can be eliminated from the remainder of the row or (as in the illustration above) column.
Virtual cross-hatching is the simplest and most obvious form of analysis. The set of cells at the intersection of a row or column with a block is special because this set of cells has 12 buddies in common.
It may be worth noting that it is not necessary that a digit be a candidate in all 3 of the cells in the intersection of the 2 regions, 2 cells works just as well. It is only necessary that the digit is not a candidate in any of the other cells in one of the intersecting regions. If there is only 1 cell of the 3 where the digit may be placed, then we should have caught that with cross-hatching.
- tuples analysis:
-
The discussion here becomes much more abstract than the
discussion up to this point. The material is presented
deductively. An inductive approach might be easier for most
people to understand, but I wished to include proof of my
assertions concerning tuples analysis so a deductive approach
is better suited to that task. Besides, I like deductive logic
as I am sure you do too since you like Sudoku. While you may be
very good at the logical deductions needed to solve a Sudoku
puzzle, trying to put into words how you did it can be tedious
and reading someone else’s description can be even worse.
So if after reading several paragraphs of this section, your
eyes begin to glaze over and your brain goes numb, try this;
scan down to the naked pairs illustration. Read the caption
and study the illustration until you understand the concept of
a naked pair. Then go back and read the sub-section on naked
pairs. Then scan down to the next illustration (hidden pairs)
and repeat the process for the sub-section on hidden pairs.
Continue down the page this way until you reach the sub-section
on Naked and Hidden “Singles”. At this point return
here and read the entire section on tuples analysis. By now the
mumbo jumbo should start to make sense.
Tuples analysis actually covers what are often identified as multiple techniques (e.g. naked and hidden pairs, naked and hidden triples, naked and hidden quads, etc.). I think you will see why it makes sense to consider them all the same basic technique when you have finished reading this.
Some other authors refer to tuples analysis as locked set analysis. I prefer the name ‘tuples’ to ‘locked sets’ because it is more compact and also I believe it is more descriptive as it generalizes the names of the variations on the tuples or locked sets theme (e.g. naked and hidden pairs, naked and hidden triples, etc.). The term ‘locked set’ will be used interchangeably with ‘naked tuple’ when describing the set of cells and candidates that forms the basis of tuples analysis because it will be needed to describe a more advanced technique (almost locked sets) based on the key concept of tuples analysis.
The key concept is the notion of a naked tuple or locked set. If a set of N empty cells in a region has exactly N distinct candidates then that set of cells and candidates forms a locked set or a naked tuple. If a set of N empty cells has less than N candidates the puzzle is unsolvable because there are not enough candidates to populate all the empty cells. If the N cells have more than N candidates, then some of those candidates must be placed in other empty cells in the region that are not part of the set because only one digit is allowed per cell. When there are exactly N candidates for N cells, then none of those candidates can be placed in a cell outside the set, because doing so would reduce the number of candidates for the set to less than N and the puzzle would be unsolvable. Whenever a locked set is identified, all candidates in the set can be eliminated from cells outside the set (but within the region).
The trivial naked tuple (or just trivial tuple) is the union of all the empty cells in a region and their candidates. Every region with one or more empty cells has a trivial naked tuple. A little reflection on the definition and discussion of naked tuples in the previous paragraph should convince you that this assertion must be true for all puzzles with a solution. For instance, a row with 5 empty cells must have exactly 5 candidates to fill those empty cells. All 5 candidates do not have to appear in each and every cell, but the union of the candidate sets of the 5 empty cells must have 5 members. If there are less than 5 candidates that is not enough to populate all the empty cells in the row and the puzzle doesn’t have a solution. There cannot be more than 5 candidates because there are only 5 empty cells in the row and nowhere else to place the extra candidates. In the discussion that follows all references to tuples exclude the trivial tuple unless otherwise noted.
Below I describe the 4 simplest instances of tuples analysis (naked and hidden pairs, naked and hidden triples) leaving the higher order instances as an exercise for the reader.
Naked Pairs: A naked pair is a locked set or naked tuple where N=2. There are 2 empty cells in a region (row, column or block) with only 2 candidates and they both have the same 2 candidates. These candidates can be eliminated from all other empty cells in the region.
The proof is easy and proceeds by contradiction. Assume we have a naked pair, but we try to place one of the candidates of the naked pair in one of the other empty cells in the region. When the candidate is placed it must be eliminated as a candidate from all the remaining empty cells in the region. This means that the empty cells of the naked pair now have only 1 candidate and that is not enough to populate both of the empty cells of the pair. Hence, the candidates of a naked pair can only be placed in the empty cells of the pair and may be eliminated from all other empty cells in the region.
In the illustration below there is a naked pair indicated by the cells with a tan background. The pair is located in the 8th row and the bottom center block. The small red digits are the candidate sets and the 8s and 9s highlighted in yellow are the candidates eliminated by the naked pair. There are 3 more (non-trivial) naked pairs in this illustration. Can you find them?
Hidden Pairs: A hidden pair exists when a pair of empty cells in a region contains 2 candidates that do not occur in any of the other empty cells of the region. A hidden pair differs from a naked pair in that there are more than 2 candidates for the pair, but only 2 are confined to the pair. A hidden pair allows us to eliminate all the other candidates from the empty cells of the pair.
Again the proof is simple and as before proceeds by contradiction. Suppose we have a hidden pair and we try to place one of the extra candidates in one of the empty cells of the pair. That means we now have only one empty cell remaining in which to place the 2 candidates that are confined to the pair, so one of those candidates cannot be placed at all. Hence only the candidates of the hidden pair may be placed in the empty cells of the pair and all other candidates can be eliminated from the pair.
In the illustration below there is a hidden pair indicated by the cells with a tan background (the candidates 7 and 8). The pair is located in the top center block. The small digits are the candidate sets and the digits shown in blue are the candidates eliminated by the hidden pair. In this illustration with the candidate sets made explicit, it is much easier to spot the complimentary naked pair (the 2s and 4s in the 1st and 3rd cells of the 6th column) in the block than the hidden pair. But without the markup, the hidden pair is easier to see. Noting that 7 and 8 do not appear in the top center block but they are given as clues at the bottom of the 6th column that leaves only 2 cells in the top center block where they could go, and so you have found the hidden pair.
Higher Order Tuples: The same concept applies to 3 cells with 3 candidates, or 4 cells with 4 candidates and so on. I will give the definitions of naked and hidden triples and let you work out the rest.
A naked triple exists when there are 3 empty cells in a region with only 3 candidates. What this means is that the combined total of all the distinct candidates in the 3 empty cells is 3. For example it would be possible that one empty cell has the digits 1 and 2 as candidates, the candidates for a second empty cell could be 2 and 3 and a third empty cell could have the candidates 1 and 3. None of those 3 cells has 3 candidates, but together the 3 cells have only 3 distinct candidates. Further, the candidates 1, 2 or 3 could also be candidates in the other empty cells of the region, but no candidates other than 1, 2 and 3 occur in the empty cells of the triple. This is an example of a naked triple (or locked set of order N=3). As with a naked pair, a naked triple allows you to eliminate the candidates of the triple from all the other empty cells of the region. This last assertion can be proved in a manner analogous to the proof for naked pairs given above and is left as an exercise for the reader.
In the illustration below there is a naked triple indicated by the cells with a tan background. The triple is located in the 3rd column. The small red digits are the candidate sets. Notice that the union of the candidate sets of the triple is (3, 8, 9), but all three candidates only appear in one cell of the triple. The key is that no candidates other than 3, 8 and 9 appear in the cells of the triple. The 9 highlighted in yellow is the candidate eliminated by the naked triple. But, if you think about it, this could just as well be done by virtual cross-hatching the 9s.
A hidden triple exists when there are 3 empty cells in a region with 3 candidates that do not occur in any of the other empty cells in the region. For example assume the same distribution of the candidates 1, 2 and 3 over 3 empty cells in a region as in the example above for naked triples, but with the following differences: there are one or more other candidates besides 1, 2 or 3 in the empty cells of the triple and the candidates 1, 2 and 3 do not occur in any of the other empty cells of the region. This is an example of a hidden triple. As with hidden pairs, a hidden triple allows you to eliminate the extra candidates from the empty cells of the triple. This last assertion can be proved in a manner analogous to the proof for hidden pairs given above and is left as an exercise for the reader.
In the illustration below there is a hidden triple indicated by the cells with a tan background (the candidates 1, 2 and 4). The triple is located in the 5th column. The small digits are the candidate sets and the digits shown in blue are the candidates eliminated by the hidden triple. The candidates 1, 2 and 4 form the triple because they only appear in the cells of the triple and not in any of the other empty cells in the 5th column. Do you see the complimentary naked triple?
Naked and Hidden “Singles”: For completeness, and possibly clarity, consider this: the missing digit scan technique could be classified as a “naked single”. Essentially, there is one empty cell in a region with only one candidate. When you discover a “naked single” you eliminate that candidate from all the other empty cells in the region. The difference is that you also place the candidate in the empty cell as its solution.
Continuing in this vein, the cross-hatching technique could be classified as a “hidden single”. Essentially, there is one empty cell in a region with one candidate that does not appear in any of the other empty cells of the region. When you discover a “hidden single” you eliminate all the other candidates from that empty cell. Again, this leads directly to a solution, where higher order hidden tuples only eliminate candidates but don’t give you a solution directly.
The Rule of Complimentary Tuples: The Rule of Complimentary Tuples states: whenever a tuple exists in a region the remaining empty cells of the region form a complimentary tuple and at least one of these tuples must be a naked tuple.
I will prove this statement in 2 stages. First I will show that a naked tuple implies that the remaining empty cells of the region must compose either a naked or hidden tuple and then I will show that a hidden tuple implies that the remaining empty cells of the region compose a naked tuple. Once these 2 propositions are established, the Rule of Complimentary Tuples is proved because we will have proved the existence of a complimentary tuple for both classes of tuples (naked and hidden) and we will have proved that at least one of the tuples is a naked tuple because either we began with a naked tuple or the existence of a hidden tuple implies that the compliment is a naked tuple.
Consider a region with N empty cells. Assume that a naked tuple of order M exists in this region. There must be N candidates for the N empty cells. Since the M cells in the naked tuple only contain M candidates (by definition) then the other N-M candidates only occur in the other N-M empty cells of the region. If some of the M candidates of the naked tuple occur in the other N-M empty cells, then those cells form a hidden tuple of order N-M because the N-M empty cells contain N-M candidates that don’t occur in any of the other empty cells of the region plus other candidates from the set of M candidates in the complimentary naked tuple. If on the other hand, none of the M candidates from the naked tuple occur in the other N-M empty cells, then those empty cells form a naked tuple of order N-M because there are exactly N-M candidates in those cells.
Now consider a region with N empty cells and assume that a hidden tuple of order M exists in this region. Since there are a total of N candidates for all N empty cells and M of those candidates are confined to the M cells of the hidden tuple, then the candidates that may occur in the other N-M empty cells are the remaining N-M candidates that are not confined to the cells of the hidden tuple. Because we have N-M cells with exactly N-M candidates the complimentary tuple is a naked tuple.
Now is a good time to point out the result of tuples analysis. If you discover a naked tuple, after eliminating the tuple candidates from the non-tuple cells, the complimentary tuple is stripped bare naked. If you discover a hidden tuple, after eliminating the non-tuple candidates from the tuple cells, the tuple is stripped bare naked and the Law of Complimentary Tuples assures us that the complimentary tuple to a hidden tuple must be a naked tuple. So, in either case the result is to partition the empty cells of the region into 2 naked tuples. The significance of this is that it doesn't matter which tuple of a complimentary pair you discover. When you have discovered one tuple of a complimentary pair and done the analysis the result is the same as if you had discovered the other and you can stop the search for tuples in that region, well almost.
One further observation is that sometimes a tuple itself can be further partitioned into complimentary pairs of tuples. This is how it is possible to have regions that contain 3 pairs. You can think of it as a pair and its complimentary quad with the quad breaking down into a pair of complimentary pairs. In fact the real benefit of tuples analysis comes when one of the complimentary tuples can be broken down further. For instance, suppose you discover a pair and its complimentary quad, then the quad breaks down further into a triple and a “single”. Remember a “single” is equivalent to either a missing digit scan or a cross-hatching scan result which fills in an empty cell with its solution. So while you may stop searching a region for tuples once you have found one, you may restart the search for tuples within each of the complimentary tuples that you have just found in the region.
There are some practical applications of this rule. If you are writing a computer program to solve Sudoku puzzles, when you implement tuples analysis you can limit the amount of computing you do. For instance, if your program starts by searching for naked and hidden pairs, then naked and hidden triples and so on, you can stop the search just before the order of the tuples exceeds half the number of empty cells in the region under consideration. You can do this with confidence because if a tuple of order greater than or equal to half the number of empty cells in the region exists it has a compliment of order less than or equal to half the number of empty cells, so by the time you reach the half way point, you will have discovered the lower order tuple in the region.
For human sudoku solvers it is often easier to spot naked tuples than hidden tuples. The rule of complimentary tuples assures us that whenever tuples exist, they come in complimentary pairs and one of the tuples in the pair must be a naked tuple, so it is only necessary to search for naked tuples. If you limit your search to naked tuples then you cannot stop the search at half the number of empty cells as in the computer programming example above, you will have to proceed up to 2 less than the number of empty cells in the region. My personal experience has convinced me that it is easier to spot a naked quad (with markups) than a hidden pair so the strategy of only looking for naked tuples could be quite helpful, at least for regions with 6 or less empty cells.






