 Click the
illustration to try an online version of the puzzle.
Click the
illustration to try an online version of the puzzle.
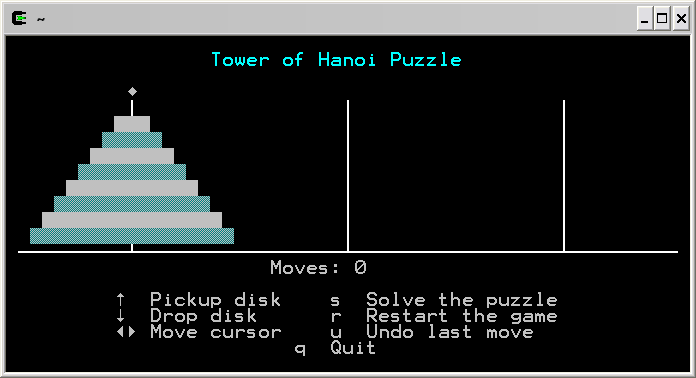
The Tower of Hanoi puzzle is often sold as a wooden puzzle consisting of a wooden base with three vertical pegs mounted on it and about 8 to 10 disks all of different sizes with a hole drilled in the center just slightly bigger than the pegs. The pegs are arranged in a row and to begin the puzzle, the disks are stacked on the left peg in order of size starting with the largest disk on the bottom moving up the stack to the smallest disk on top. This stack forms a roughly conically shaped “tower”. The object is to move the “tower” from the left peg to the right peg by moving one disk at a time to any of the 3 pegs. The only restriction is that no disk may ever be placed on top of a disk smaller than itself.
This puzzle is cited in virtually every programming textbook as the classic example of recursion. The recursive method of solution is simple. If, as in the screen shot above, we start with the problem of moving the 8 disk “tower” to the right peg from the left peg, we assume that we know how to solve the puzzle for a 7 disk “tower”. The solution is then to move the 7 disk “reduced tower” from on top of the biggest disk to the center peg, move the biggest disk from the left peg to the right peg, then move the 7 disk “reduced tower” from the center peg and put it on top of the big disk on the right peg. The solution to the 7 disk problem is accomplished in a similar manner by assuming that we know the solution to the 6 disk problem. Recursion continues until we get to the problem of moving a 1 disk “tower”. At that point we actually do know how to move 1 disk and recursion ceases. Here is the solution expressed in pseudo-code:
moveTower ( towerHeight, source, destination )
{
if ( towerHeight > 0 ) {
otherPeg = OTHER_PEG ( source, destination )
moveTower ( towerHeight-1, source, otherPeg )
moveDisk ( source, destination )
moveTower ( towerHeight-1, otherPeg, destination )
}
}The pseudo-code above sketches out a subroutine for moving a
“tower“ of disks from one peg to another without
violating the rule that a disk cannot be placed on top of a disk
smaller than itself. This routine is told how many disks are in the
“tower” by the towerHeight parameter. The
starting or source peg is indicated by the source
parameter and the destination peg is indicated by the
destination parameter. We assume there is a subroutine
(or macro) called OTHER_PEG() that takes the
source and destination parameters and returns
the other peg, the one not involved in the move. In other words,
other_peg is the peg where we will move the “reduced
tower” on top of the bottom disk to get it out of the way so we
can move the bottom disk from the source peg to the
destination peg. The defining feature of a recursive
subroutine is that it calls itself. As you can see, the
moveTower() subroutine calls itself twice. When the
towerHeight has been reduced to 0 (or less) the
moveTower() subroutine becomes a no-op. This is
important, because if we did not check for this condition the
recursion would never end, meaning the subroutine would keep calling
itself forever and never return. The following call to
moveTower() solves a puzzle that begins with an 8 disk
“tower” located on the left peg.
moveTower ( 8, LEFT_PEG, RIGHT_PEG )The moveTower() routine assumes that there actually
is a “tower” of disks on the source peg when you call it.
If the assumption is wrong, the routine fails to generate a correct
sequence of moves to solve the puzzle starting from its current
state. In my solution module given below, the assumption is relaxed
to only require that the disks are in a legal state, meaning that no
disk is on top of a disk smaller than itself. I was able to relax the
assumption concerning disk location by a small modification of the
solution algorithm discussed above. This allows my solution module to
solve the puzzle from any state that can be reached by a sequence of
legal moves beginning with the starting position of the
“tower” on the left peg. In other words, after a player
tires of attempting to solve the puzzle, he can ask for help and my
solution algorithm will demonstrate the solution starting from the
point where the player gave up.
Below is my implementation of the Tower of Hanoi puzzle using the curses library to display the puzzle with character graphics. The program allows a player to interactively move disks using the arrow keys on the keyboard to attempt to solve the puzzle. If the player gives up, he can press ‘s’ to have the computer complete the puzzle. As with the Sudoku Solver, this is written in C for Linux or Cygwin, but should work on most Unix systems with some small tweaks.
As a matter of good coding practice the code has been partitioned into modules that implement an interactive game interface, the puzzle object with display and animation logic, a command line interface and a solution module. The solution module could have been part of the puzzle object, but by keeping it separate, this code can be adapted to the classroom. An instructor could compile everything except the solution logic into a library and present his students with the problem of writing the solution logic. A makefile is provided (makelib) to compile a library and another (student_make) to compile the student’s solution module and link it with the library to create a fully functional Tower of Hanoi program.
| File Name | Description |
|---|---|
| game.c | Interface logic for interactive play. |
| hanoi.c | Command line interface, main program. |
| hanoi.h | Header file, macros and function prototypes. |
| puzzle.c | Display and animation logic. |
| solution.c | Solution logic. |
| makefile | Make file (for Linux and Cygwin). |
| hanoi_2.2 | Shell archive, contains the files above, requires uudecode, cpio and bzip2 to extract the contents. (Some Unix shells may not process DOS files correctly, so be sure to strip out the carriage returns.) |
Make files for classroom use. |
|
| makelib | Make file to build a library for instructional use. |
| student_make | Make file for the student to build his homework. |






